作者:Steven Yue,原刊于作者知乎
上一期文章中,我们一起学习了全同态加密(FHE)的定义和具体的几个阶段,并且也回顾了FHE的历史。到这里,大家应该对FHE系统已经有一个比较初步的了解了。(可点击《初探全同态加密:FHE的定义与历史回顾》查看原文)
我们在上一篇文章的结尾提到了GSW系统,也就是我们所说的第三代全同态加密系统。GSW系统的构造主要是基于格密码学中有名的LWE问题假设。为了更加方便与我们来了解GSW系统的具体构造,我们这期文章来快速地学习一下,格密码学与LWE问题究竟是什么。
格密码学(Lattice-based Crypto)是现在比较火的一个密码学分支,而且本身拥有抵抗量子计算的特性。在即将到来的NIST后量子时代加密算法标准化讨论中,基于格的加密体系就是其中的一个选择之一。不过大家不要被这些定义吓到了,其实想要理解格密码学非常简单,我们只需要一些最基本的线性代数知识。
PS:如果对线性代数内容比较生疏的话,笔者强烈建议去看3Blue1Brown大神的视频合集线性代数的本质。视频里面非常生动的描述了线性代数的基本定理。
格密码学快速入门
到底什么是格密码学?听了半天想必大家还没搞明白,其实格密码学就是基于格(Lattice)和格上的一些问题而定义的一套密码学体系。所以我们需要先搞明白,格到底是什么。
为了更加方便的举例子,我们这里介绍一个最简单的格系统——整数格(Integer Lattice)。
整数格(Integer Lattice)的构造






PS:格密码学中还有另一个难题叫SVP问题(Shortest Vector Problem),和CVP不同,但也是NP-hard的问题。我们在这里就不多解释了。

Learning With Error(LWE)问题
读到这里,想必大家应该对整数格已经有了一个大致的理解,并且也知道了整数格中的一个难问题:CVP问题。现在我们一起来看看,如何从CVP问题出发,衍生到我们的主角LWE问题上。为了更加方便理解LWE,我们不妨先来回顾一下中学数学~
我们在初中或者高中的数学课上应该都学过如何求解线性方程组(solve system of equations)。一般来说,我们会给到一组多元一次方程:


有噪音的高斯消除问题(Gaussian Elimination with Noise)
当我们学会如何求解线性方程组之后,我们发现这其实并不是什么难的问题,只需要不停地在行与行之间相互使用高斯消除,就可以得到未知数的解。毕竟这也是中学的时候学的数学题,难不到哪里去。
现在,我们把这个高斯消除问题变化一下,给它增加一些难度:增加噪音。







Diffie-Hellman公钥交换中的离散对数问题(Dlog Problem)
看到这里,对密码学熟悉的朋友们可能会对一个问题的多种版本(如搜索、决策)等等并不陌生。没错,在我们学习Diffie-Hellman公钥交换问题的时候,我们也使用了相同的问题转换。如果不了解的朋友也不用着急,容我解释一波。



DLWE与DDH的困难度比较
为什么我们要长篇大论的扯DDH问题呢?这是因为,了解了SLWE/DLWE与CDH/DDH这两对密码学中被认为困难的问题之后,我们可以来比较他们的困难度分布到底是怎么样的。
DDH假设其实非常的不完美,甚至于令人头疼。因为Pairing这个后门的存在,这直接给DDH问题设置了一个惊人的困难度下限——在Pairing存在的组中,DDH问题太简单了。所以我们在挑选群的时候,一定要精心挑选。DDH的大哥CDH却不一样,因为没有任何高效率的算法可以破解离散对数,所以在任何循环群中的复杂度都较为平均。这样一来,CDH就算再困难,对于DDH的困难度分布也没有太多实质性的帮助。我们往往需要使用平均困难度来定义DDH问题的困难度(因为下限太低了)。这在密码学中是一件非常膈应人的事情,就像是我送给你一辆车,但是告诉你这个车,有一定的可能性会一开就自动散架一样。
相比起来,LWE问题就完美许多。因为没有任何像Pairing一样的后门的存在,所以DLWE问题其实和SLWE的困难度是相同的。因为不管是解决DLWE还是SLWE,我们都会被卡在如何还原未知向量S这一步上面。像这一类就算问题形式被转换,但是复杂度保证大致相同的问题,在密码学中是不可多得的宝贝。对于DLWE问题的困难度,我们可以很优雅的使用最坏困难度(Worst Case Performance)来定义。
这一段其实多少都是密码学界大家的情怀,有一个干净的定义比搞一堆乱七八糟的假设来的舒服多了。这也就是为什么格密码学那么的吸引人的原因。不过,这些关于困难度/复杂度的小情绪,对于我们理解全同态加密是无关紧要的。大家可以当作茶余饭后的趣闻,随便看看。
DLWE的实战应用:格密码学与Regev加密算法
如果你成功的啃完了前面的干货,看到了这里,那么恭喜你,现在你已经掌握了LWE与格密码学的基础了!
现在,当我们学会了这么多知识之后,我们可以结合一下之前学习的内容,融会贯通一下, 来看看如何使用LWE问题来构建一个格密码学中常见的公钥加密系统——Regev加密算法。
Regev加密是一个叫Regev的大佬在2005年发明出来的,是一个非常类似于ElGamal类型的公钥加密系统,基于了DLWE的假设。我们来看看它的具体定义吧:




Regev加密的安全性
刚才属性的话题讨论到一半,我们打了个岔。最后我们回来继续学习一下,Regev加密系统的安全性(Security)。
为了证明Regev加密体系是语义安全的,我们需要使用密码学中的一种常见的证明工具:混合论证法(Hybrid Argument)。混合论证其实并不是什么黑科技,而是我们把要证明的问题划分成若干小步,然后逐步证明罢了。
首先,我们来看一下,假如一个第三方偷看到了Regev加密系统的加密密文的所有消息,那么他的世界观是这样的:

接着,我们可以创建第二个相似的世界观:
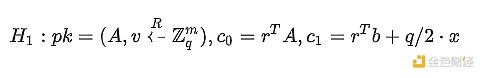


未完待续:构建有限级数全同态算法
最后,我们来回顾一下这一期的内容~
首先,我们一起看到了整数格(Integer Lattice)的定义,然后基于整数格了解了NP-hard的最近向量问题( CVP)。随后,我们重新回顾了高中时期学习的求解线性方程组问题,并且统一归纳为高斯消除问题。随后,我们给高斯消除问题本身加入了一个随机的误差噪音,从而构成了我们的主角,误差还原(LWE)问题。
了解了LWE是什么之后,我们又详细学习了LWE问题的正式定义,以及其中的n,m,q,B参数。接着我们把搜索LWE(SLWE)转换为决策LWE(DLWE)问题,然后探讨了SLWE/DLWE的假设为什么比CDH/DDH更好。最后,我们结合了所有学习的知识,一起构建了格密码学中很经典的Regev加密算法,通过LWE的困难假设对密文(一个bit)进行加密。
如果你读到这里,并且成功的理解了所有的内容的话,那么其实你已经掌握了全同态加密80%的精髓了!接下来,我们需要做的只是把这些部分像搭积木一样搭起来,就可以构成我们想要的全同态加密系统了。
由于篇幅原因,我们这一期就写到这里。下一期,我们使用这期学到的知识,一起来构建一个有限级数全同态加密体系。





