作者:Vitalik Buterin;编译:布噜说
在 The Three Transitions 这篇文章中,以太坊创始人 Vitalik Buterin 明确地阐述了有关「主网(下文简称 L1)+ 第 2 层跨链(下文简称 cross-L2)支持」「钱包安全」和「隐私」作为生态系统堆栈必要功能的重要价值,它们不该只是一些附加的组件,由单独的钱包提供相关的功能。
而本篇文章,Vitalik Buterin 指出,将重点探讨一个关键的技术问题:如何能够更容易地从 L2 读取 L1 的数据;或者从 L1 读取 L2 的数据;或者如何更容易地从一个 L2 读取另一个 L2 的数据。
Vitalik Buterin 指出,解决上述问题的关键在于,如何实现资产与密钥库的分离架构。这个技术在扩容以外的领域也有非常有价值的用例,比如 L1 和 L2 之间资产的移动互通。
这样做的目标是什么?
一旦 L2 成为主流,用户将能够在多个 L2 上拥有资产,也可能在 L1 上拥有资产。
一旦智能合约钱包成为主流,现在常见的「密钥」将不再被使用。
而一旦这两件事情同时发生,用户就会需要一种不需要伴随大量交易的方法,来更换不同账户的密钥。
尤其是,我们需要一种方法来处理那些「反事实设定」的地址(也可以理解成「假设地址」):这是一些尚未以任何方式在链上「注册」的地址,但仍需要接收并安全地持有资产。
事实上,我们都依赖于这种「反事实设定」的地址:当用户第一次使用以太坊时,用户可以生成一个 ETH 地址,他人可以向这个账户支付,而无需在区块链上「注册」该地址(但会需要支付交易费用,因此需要持有若干 ETH)。
对于外部账户(EOA)而言,其实所有的地址都是从「反事实设定」的地址开始的。
对于智能合约钱包,「反事实设定」的地址仍然是可能的,这在很大程度上要归功于 CREATE2,它允许您拥有一个 ETH 地址,只能由与特定哈希值匹配的智能合约代码填充。
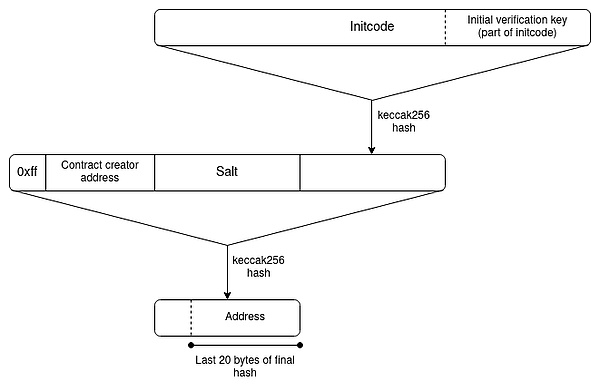
△ EIP-1014(CREATE2)地址计算算法。
然而,引入智能合约钱包,也带来了新的挑战:访问密钥可能发生变化。这个变化在于,地址是 initcode 的哈希值,只能包含钱包的初始验证密钥,而当前的验证密钥将存储在钱包的存储中,但该存储记录不会自动转移到其他 L2 中。
如果一个用户在许多 L2 上都有地址,这时候就只有资产与密钥存储分离架构可以帮助用户更改他们的密钥了。
这个分离架构的结构是:每个用户都有(i)一个「密钥存储合约」(在 L1 或特定的 L2 链上),它存储了所有钱包的验证密钥以及更改密钥的规则,以及(ii)在 L1 和许多 L2 链上的「钱包合约」,它们通过跨链读取来获取验证密钥。
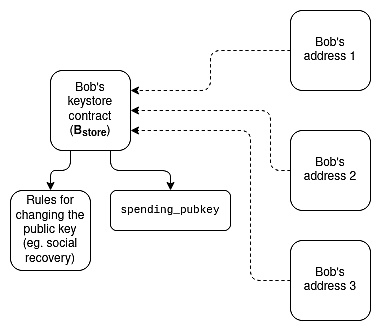
资产与密钥存储分离架构有两种实现方法:
轻量级版本(即仅检查更新密钥):每个钱包在本地存储验证密钥,并包含一个可调用的函数来检查密钥库当前状态的跨链证明,并更新本地存储的验证密钥以匹配。在某个 L2 上首次使用钱包时,调用该函数从密钥库获取当前的验证密钥是必需的。
优点:对跨链证明的使用较为审慎,不会出现太昂贵的网络操作费用。所有资产只能通过当前密钥使用,因此安全性仍然得到保证。
缺点:需要更改验证密钥,必须在密钥库和已初始化的每个钱包上进行链上密钥更改,可能需要消耗很多 Gas Fee。
完整版本(即每个交易都检查):每笔交易都需要一个跨链证明,显示密钥库中的当前密钥。
优点:系统复杂性较低,且密钥库更新迅速。
缺点:单个交易的网络操作费用较高,不容易与 ERC-4337 兼容,ERC-4337 目前尚不支持在验证期间跨合约读取可变对象。
什么是跨链证明?
为了展示跨链证明的复杂性,我们选取了一种最复杂的应用场景作为展示解释这个技术原理,这个复杂的应用场景如下:密钥存储在一个 L2 上,而钱包在另一个 L2 上。如果钱包上的密钥库在 L1 上,那么只需要此设计的一半。
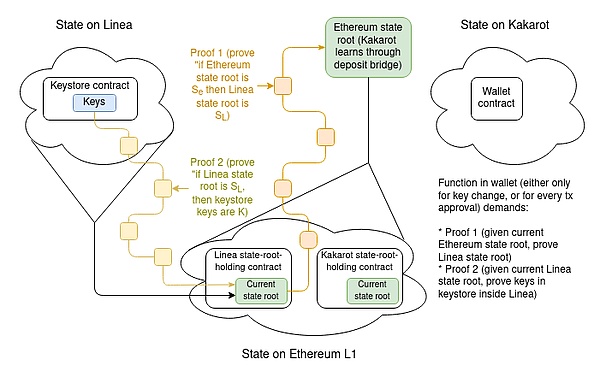
假设密钥库在 Linea 上,钱包在 Kakarot 上。钱包密钥的完整证明过程则需要包括:
证明当前 Linea 状态根的证明,给定 Kakarot 知道的当前以太坊状态根。
证明密钥库中当前密钥的证明,给定当前 Linea 状态根。
这里有两个主要的棘手的实现问题:「需要使用什么样的证据?(是默克尔证明吗?还是别的什么?)」以及 「L2 如何学习最近的 L1 状态根?」或者,「L1 如何学习 L2 的状态根?」
那么,在这两种情况下,一方发生某事件后,到另一方能够提供证明之间,会有多长的延迟时间?
我们可以使用哪些证明方案?
主要有五种方法可供选择:
Merkle 证明
通用 ZK-SNARKs
特殊目的证明(例如,使用 KZG)
Verkle 证明,介于 KZG 和 ZK-SNARKs 之间,既考虑基础设施工作量又考虑成本
没有证明,依赖直接状态读取
就所需的基础设施工作和用户成本而言,大致可将它们进行如下排列比较:
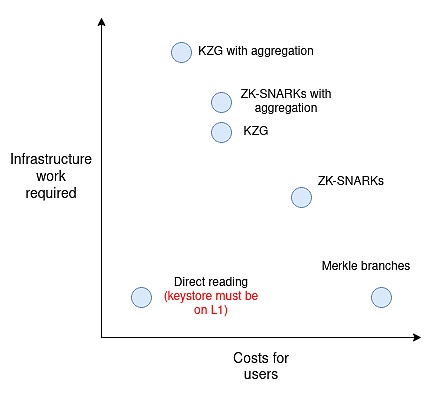
「聚合」是指将每个区块中用户提供的所有证明聚合成一个大的元证明,将它们合并在一起。这对于 SNARKs 和 KZG 是可行的,但对于 Merkle 分支来说不行。
事实上,只有当方案拥有大量用户时,「聚合」才能体现价值。
Merkle 证明是如何工作的?
这个问题很简单,可以直接按照上一节的图表。每个 「证明」(假设是将一个 L2 证明为另一个 L2 ,这是难度最大的一种应用场景)将包括:
一个 Merkle 分支,证明了持有 L2 键库的状态根,根据 L2 所知道的以太坊的最新状态根。持有 L2 键库的状态根存储在已知地址(代表 L2 的 L1 合约)的已知存储槽中,因此可以将路径硬编码。
一个 Merkle 分支,证明了当前的验证密钥,根据持有 L2 键库的状态根。同样,验证密钥存储在已知地址的已知存储槽中,因此路径可以硬编码。
然而,以太坊的状态证明很复杂,但是有一些库可以用来验证它们,如果使用这些库,这个机制并不太复杂。
不过,更大的挑战是成本问题。Merkle 证明很长,而 Patricia 树比必要的就是长 3.9 倍——远远高于目前每笔交易 2.1万个 Gas Fee 的基本价格。
但是,如果在 L2 上验证证明,则差异会变得更糟。L2 内部的计算很便宜,因为计算是在链下完成的,并且是在节点大量少于 L1 的生态系统里完成。
我们可以通过查看 L1 Gas Fee 成本和 L2 Gas Fee 成本之间的比较来计算这意味着什么:
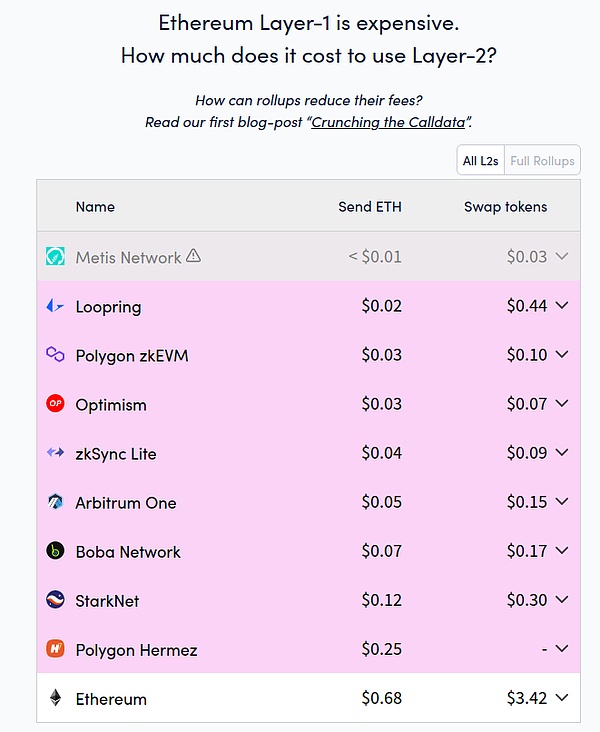
当下,如果是较为简单的发送操作,L1 网络上的成本大约是 L2 的 15~25 倍,而 Token 交换的成本则大约是 L2 的 20~50 倍。
简单的发送操作,数据量较大;而交换操作对于算力的要求更高,因此,交换操作是一个更好的基准来近似 L1 计算与 L2 计算的成本。
综合考虑以上情况,如果我们假设 L1 计算成本和 L2 计算成本之间的成本比为 30 倍,这似乎意味着将 Merkle 证明放在 L2 上的成本可能相当于大约五十个常规交易。
当然,使用二进制 Merkle 树可以减少成本约为 4 倍,但即使如此,在大多数情况下,成本仍然会过高 ,而且如果我们愿意放弃与以太坊当前的六进制状态树的兼容性,可能还会寻求更好的选择。
ZK-SNARK 证明是如何工作的?
从概念上讲,ZK-SNARK 的使用也很容易理解:您只需将上图中的 Merkle 证明替换为证明这些 Merkle 证明存在的 ZK-SNARK。一个 ZK-SNARK 的计算量约为400,000 Gas Fee,约 400 字节;一个基本事务需要 21,000 个 Gas Fee 和 100 个字节。
因此,从计算角度看,ZK-SNARK 的成本是现在基本交易成本的 19 倍;从数据角度看,ZK-SNARK 的成本是现在基本交易成本的 4 倍,是未来基本交易成本的 16 倍。
这些数字与 Merkle 证明相比有了巨大的改进,但仍然相当昂贵。有两种方法可以改善这种情况:(i) 特殊用途的 KZG 证明,或(ii) 聚合,类似于 ERC-4337 聚合。
特殊用途的 KZG 证明如何工作?
首先,回顾一下 KZG 承诺的工作原理:
[D_1 ...D_n] 表示一组数据,通过这组数据导出多项式 KZG 证明。
具体来说,多项式 P,其中 P(w) = D_1,P(w²) = D_2 ...P(wⁿ) = D_n. w 这里是「统一根」,对于某些评估域大小 N,wN = 1 的值(这一切都是在有限域中完成的)。
为了「提交」到 P,我们创建一个椭圆曲线点 com(P) = P₀ * G + P₁ * S₁ + ... + Pk * Sk。这里:
G 是曲线的生成器点
Pi 是多项式 P 的第 i 次系数
Si 是可信设置中的第 i 个点
而为了证明 P(z) = a,我们创建一个商多项式 Q = (P - a) / (X - z),并创建一个承诺 com(Q)。只有当 P(z) 实际上等于 a 时,才有可能创建这样的多项式。
为了验证证明,我们通过对证明 com(Q) 和多项式承诺 com(P) 进行椭圆曲线检查来检查方程 Q * (X - z) = P - a:我们检查 e(com(Q), com(X - z)) ?= e(com(P) - com(a), com(1))
还需要了解的一些关键属性包括:
证明只是 com(Q) 值,即 48 个字节
com(P₁) + com(P₂) = com(P₁ + P₂)
这也意味着您可以将值「编辑」为现有合约。
假设我们知道 D_i 当前是 a,我们希望将其设置为 b,并且对 D 的现有承诺是 com(P)。承诺“P,但 P(wⁱ) = b,并且没有其他评估更改”,然后我们设置 com(new_P) = com(P) + (b-a) * com(Li),其中 Li 是「拉格朗日多项式」,在 wⁱ 处等于 1,在其他 wj 点处等于 0。
为了有效地执行这些更新,每个客户端都可以预先计算和存储对拉格朗日多项式 (com(Li)) 的所有 N 个承诺。在链上合约中,存储所有 N 个承诺可能太多了,所以你可以对 com(L_i)值集做出 KZG 承诺,所以每当有人需要更新链上的树时,他们可以简单地向适当的 com(L_i) 提供其正确性的证明。
因此,有一个结构可以继续将值添加到不断增长的列表的末尾,但有一定的大小限制。然后,使用这个结构作为数据结构(i)对每个 L2 上的密钥列表的承诺,存储在该 L2 上并镜像到 L1,以及(ii)对 L2 密钥承诺列表的承诺,存储在以太坊 L1 上并镜像到每个 L2。
保持承诺更新可以成为核心 L2 逻辑的一部分,也可以通过存款和撤回桥接实现,而无需更改 L2 核心协议。
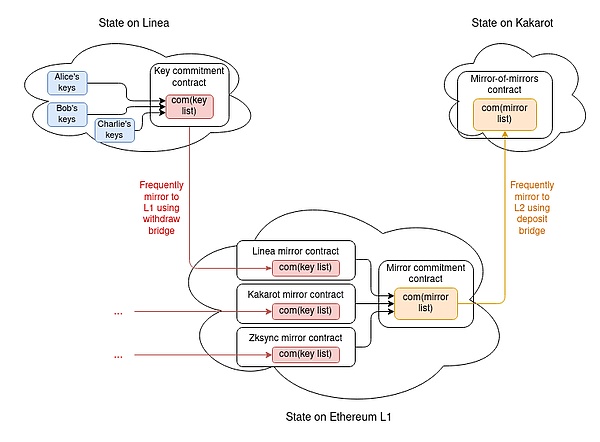
一份完整的证明所需的内容如下:
存放 L2 上密钥库的最新 com(密钥列表)。
将 com(密钥列表)作为 com(镜像列表)中的值的 KZG 证明,com(镜像列表)是所有密钥列表承诺的列表。
将用户的密钥在 com(密钥列表)中进行 KZG 证明。
事实上,上述两个 KZG 证明可以合并为一个,总大小只有 100 字节。
请注意一个细节:由于密钥列表是一个列表,而不是像状态那样的键/值映射,密钥列表必须按顺序分配位置。密钥承诺合约将包含其自己的内部注册表,将每个密钥库映射到一个 ID,并且对于每个密钥,它将存储 hash(key,密钥库的地址)而不仅仅是 key,以明确地告知其他 L2 关于特定条目所指的密钥库。
这种技术的优点是在 L2 上性能非常好。比 ZK-SNARK 短约 4 倍,比 Merkle 证明短得多。计算成本大约为119,000 Gas Fee。
在 L1 上,算力比数据更重要,因此 KZG 比 Merkle 证明要稍微昂贵一些。
Verkle 树如何工作?
Verkle 树本质上涉及将 KZG 承诺堆叠在一起:要存储 2⁴⁸ 值,可以对 2²⁴ 值列表做出 KZG 承诺,每个值本身都是 KZG 对 2²⁴ 值的承诺。
Verkle 树被考虑用于以太坊状态树,因为 Verkle 树可以用来保存键值映射。
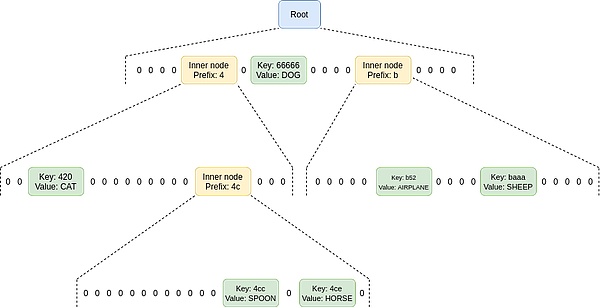
Verkle 树中的证明比 KZG 证明更长,它们可能有几百个字节长。
实际上,Verkle 树应该被认为是像 Merkle 树,但如果没有 SNARKing 更可行,但 SNARKing 被证明有更低的证明成本。
Verkle 树的最大优点是可以协调数据结构:因此可以直接用于 L1 或 L2,没有叠加结构,并且对 L1 和 L2 使用完全相同的机制。
一旦量子计算机成为一个问题,或者一旦证明 Merkle 分支变得足够高效,Verkle 树就有了更多地用武之地。
聚合
如果 N 个用户做了 N 笔交易,需要证明 N 个跨链索赔,我们可以通过聚合这些证明来节省大量的 Gas Fee,这可能意味着:
一个 N 个 Merkle 分支的 ZK-SNARK 证明
一个 KZG 多重证明
一个 Verkle 多重证明(或一个多重证明的 ZK-SNARK)
在所有这三种情况下,每个证明只需花费几十万 Gas Fee。
开发者需要在每个 L2 上为该 L2 的用户制作一个这样的证明;因此,为了使这个证明有用,整个计划需要有足够的使用量,以至于在多个主要 L2 的同一区块内经常有至少几个交易。
如果使用 ZK-SNARKs,每个用户可能需要花费几千个 L2 Gas Fee。如果使用 KZG 多重证明,验证者需要为该区块内使用的每个持有钥匙库的 L2 增加 48 个Gas Fee。
不过,这些成本比不聚合的成本要低得多,后者不可避免地涉及到每个用户超过 10000 个 L1 Gas Fee 和数十万个 L2 Gas Fee。
对于 Verkle 树,用户可以直接使用 Verkle 多证明,每个用户增加大约 100~200 字节,或者你可以做一个 Verkle 多证明的 ZK-SNARK,它的成本与 Merkle 分支的 ZK-SNARK 相似,但证明起来明显便宜。
从实施的角度来看,让捆绑者通过 ERC-4337 账户抽象标准聚合跨链证明可能是最好的。ERC-4337 已经有一个机制,让构建者以自定义的方式聚合 User Operations 的部分。甚至有一个针对 BLS 签名聚合的实现,这可以将 L2 的 Gas Fee 降低 1.5 倍到 3 倍。
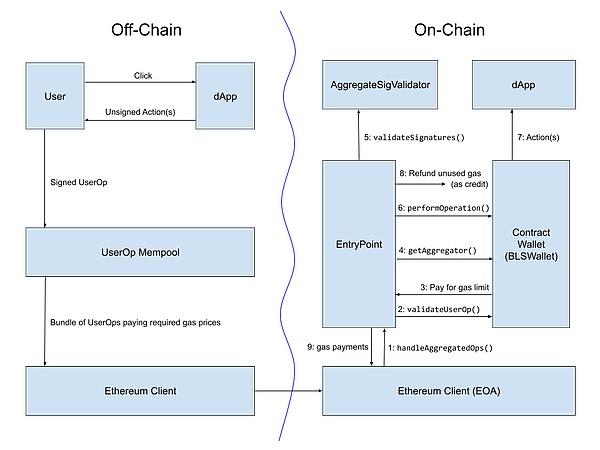
直接读取状态
最后一种可能,也是只适用于 L2 读 L1(而不是 L1 读 L2)的一种可能,就是修改 L2,让它们直接对 L1 的合约进行静态调用。
这可以通过一个操作码或预编译来实现,它允许调用 L1,你提供目标地址、气体和 calldata,然后它返回输出,尽管由于这些调用是静态调用,它们实际上不能改变任何 L1 状态。L2 必须知道 L1 的情况才能处理存款,所以没有什么根本性的东西可以阻止这种东西的实现;这主要是一个技术实现上的挑战。
请注意,如果密钥库在 L1 上,并且 L2 整合了 L1 的静态调用功能,那么就根本不需要证明。
但是,如果 L2 没有整合 L1 静态调用,或者如果密钥库在 L2 上,那么就需要证明了。
L2 如何学习最近的以太坊状态根?
上述所有方案都要求 L2 访问最近的 L1 状态根或整个最近的 L1 状态。
事实上,如果 L2 具有存入功能,那么您可以按原样使用该 L2 将 L1 状态根移动到 L2 上的合约中:只需让 L1 上的合约调用 BLOCKHASH 操作码,并将其作为资产存入的消息传递给 L2。可以在 L2 端接收完整的块标头,并提取其状态根。
但是,每个 L2 最好都有明确的方式来直接访问完整的最新 L1 状态或最近的 L1 状态根。
优化 L2 接收最新 L1 状态根的方式的主要挑战是同时实现安全性和低延迟:
如果 L2 缓慢实现直接读取 L1 功能,只读取最终的 L1 状态根,那么延迟通常为 15 分钟,但在一些极端情况下,延迟可能是几周。
L2 绝对可以设计为读取更新的 L1 状态根,但由于 L1 可以恢复(即使具有单插槽终结性,在非活动泄漏期间也会发生恢复),L2 也需要能够恢复。从软件工程的角度来看,这在技术上具有挑战性。
如果使用桥将 L1 状态根引入 L2,那么资产更新需要花费很长的时间,在最好的情况下,不断有用户支付更新费用,并使系统为其他人保持最新状态。
不过,「预言机」(Oracles)在这里不是一个可接受的解决方案:钱包密钥管理是一个非常安全的关键低级功能,因此它最多应该依赖于几个非常简单的、无需加密信任的低级基础设施。
此外,在相反的方向上(L1 读取 L2):
在 Optimistic Rollup 中,由于欺诈证明延迟,州根需要一周才能达到 L1。在 ZK 汇总中,由于验证时间和经济限制的结合,现在需要几个小时,尽管未来的技术将减少这种情况。
预确认(来自测序仪、证明者等)不是 L1 读数 L2 的可接受解决方案。钱包管理是一个非常安全关键的低级功能,因此 L2 到 L1 的通信安全级别必须是绝对的高。L1 应信任的唯一状态根是已被 L2 在 L1 上的状态根持有合约接受为最终状态根。
对于许多 DeFi 用例来说,其中一些用于无信任跨链操作的速度慢得令人无法接受。然而,对于更新钱包密钥的用例,更长的延迟更容易接受——因为不是延迟交易,是延迟密钥更改。
用户只需要将旧密钥保留更长时间即可。如果用户因为密钥被盗而更改密钥,那么确实有很长一段时间的漏洞,但可以缓解,例如。通过具有冻结功能的钱包。
最终,最好的延迟最小化解决方案是让 L2 以最佳方式实现对 L1 状态根的直接读取,其中每个 L2 块(或状态根计算日志)包含一个指向最新 L1 块的指针,因此如果 L1 恢复,L2 也可以恢复。密钥库合约应放置在主网上或 ZK-rollup 的 L2 上,以便可以快速提交到 L1。
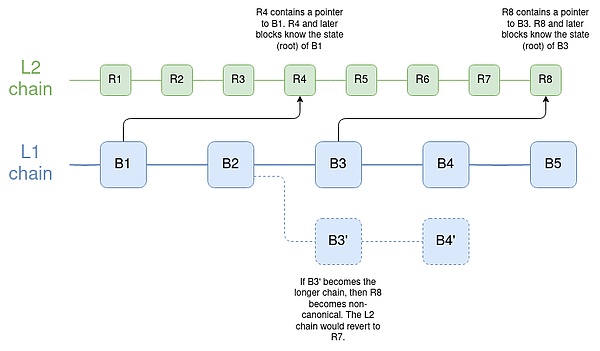
另一个链需要多少与以太坊有多少连接,才能持有密钥库存储在以太坊或 L2 的钱包?
令人惊讶的是,没有那么多。实际上,它甚至不需要是一个 Rollup。
如果它是一个 L3,或者是一个 validium,那么在那里存放钱包也是可以的,只要用户在 L1 或 ZK-rollup 上存放密钥存储,确实需要能够直接访问以太坊的状态根,以及愿意在以太坊重构时,在以太坊硬分叉时进行硬分叉。
基于 ZK 桥的方案有吸引人的技术特性,但它们有一个关键的弱点,即它们对 51% 攻击或硬分叉不健全。
保护隐私
理想情况下,用户还希望保护隐私。如果一个用户有许多由同一个密钥库管理的钱包,那么他们希望确保:
不让公众知道这些钱包都是相互连接的。
社交恢复监护人不会了解他们所监护的地址是什么。
但这就产生了一下问题:
我们不能直接使用 Merkle 证明,因为它们不能保护隐私。
如果我们使用 KZG 或 SNARKs,那么证明需要提供验证密钥的盲版,而不泄露验证密钥的位置。
如果我们使用聚合,那么聚合器就不应该以明文的方式了解位置;相反,聚合器应该接收盲证明,并有办法聚合这些证明。
我们不能使用「轻量级版本」(仅在更新密钥时使用跨链证明),因为这会造成隐私泄露:如果许多钱包由于更新程序而同时更新,那么时间上就会泄露这些钱包可能相关的信息。因此,我们必须使用 「完整版本」(对每笔交易进行跨链证明)。
对于 SNARKs,解决方案在概念上很简单:默认情况下证明是信息隐藏的,聚合器需要产生递归 SNARK 来证明 SNARKs。
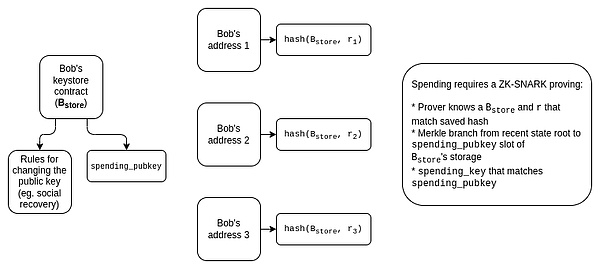
这种方法目前面临的主要挑战是:聚合需要聚合器创建一个递归的 SNARK,速度上相当慢。
对于 KZG,我们可以使用非索引揭示 KZG 证明的工作。然而,盲证的聚合是一个开放的问题,需要更多的关注。
不过,虽然从 L2 内部直接读取 L1 并不能保护隐私,但实现这个直接读取功能仍然将非常有用——不仅因为可以最大限度地减少延迟,还可以用于其他更多用例。





